Application of the Theorem with a Conceptual Understanding
Mathematics is a perfect opportunity for practical thinking and application. Unfortunately, kids are caught in situations where they are attempting to apply practically but their absent of the practical thinking. Without the understanding of the concept, students depend on their application of formulas. This can produce the right answer, but the mathematical thinking may be compromised. When students learn math conceptually, they are able to utilize their knowledge and experiences from academic and practical mathematics. The Pythagorean Theorem is a perfect example of a formula that is often used as a means to find the right answer. In reality, it is a theorem that is the epitome of a formula created from conceptual mathematic thinking.
Who is Pythagoras?

Regarded to many as the Father of Mathematics, Pythagoras, a Greek Philosopher once said, “Educate the children and it won’t be necessary to punish the men.” Pythagoras was intrigued with and a learner of many things (numbers, arithmetic, geometry, just to name a few). Unfortunately, he and his group of learners were very secretive and they did not document any of his teachings. Like the Pythagorean Theorem, what we know about Pythagoras was written by other philosophers, hundreds of years after his death.
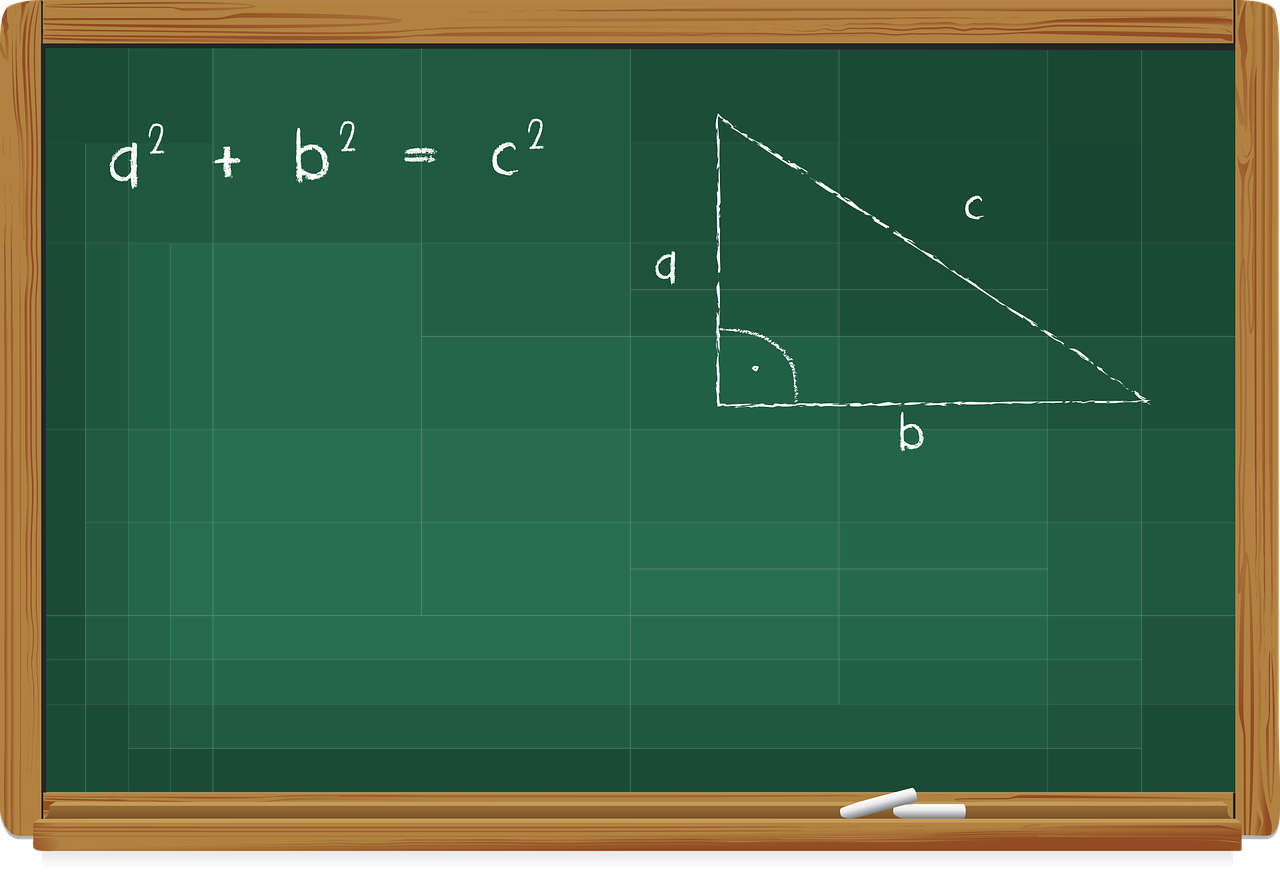
Much of what Pythagoras knew about triangles derived from his studies of Ancient Egyptian, Babylonian and Chinese mathematics. Pythagoras took all of his knowledge and created a proof, or the Pythagorean Theorem. In short, Pythagoras proved that the work of the Ancient Mathematicians worked. Pythagoras solidified that for any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two legs. We know this as the equation a2 + b2 = c2.
The Conceptual Math Leading to The Pythagorean Theorem
Where Did the 2 (Squared) Come From?
Since the formula has the superscripted 2s next to each variable (letters a, b, and c), that tells us that we are dealing with square roots or the power of 2. Asking for the square root of 9 or √9 is the same thing as answering what number multiplied by itself is 9. So the square root of 9 is 3. For our kids to think conceptually through the formula, they have to catch the key word, “square”.
When kids are just taught the formula to find a missing side of a right triangle, they don’t see that the Theorem has so much to do with squares as much as right triangles. This is the same conceptual thinking that Pythagoras used to come up with his proof. Consider the following diagram:
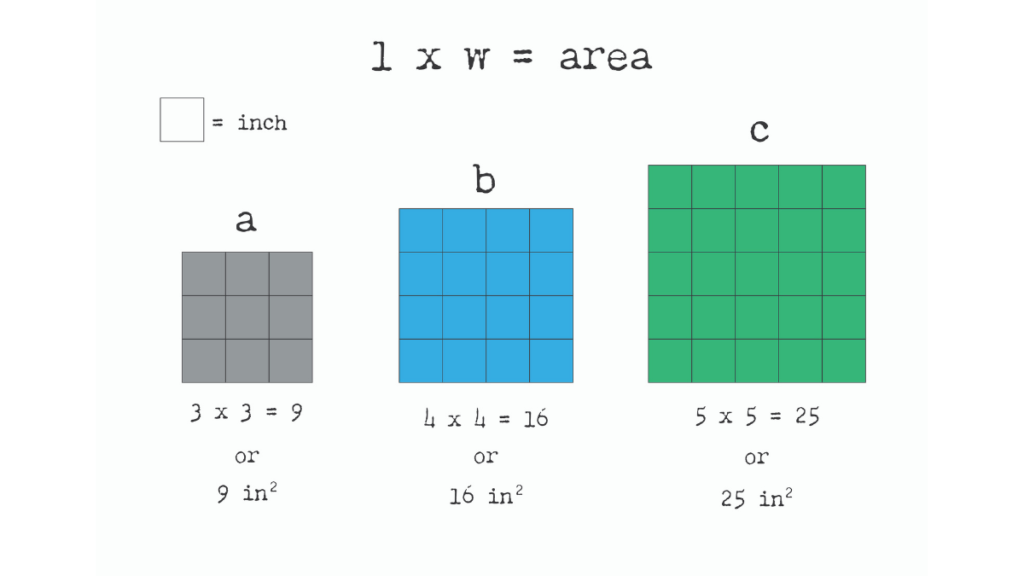
At this point in mathematics kids should know how to find the area of squares fairly well. Square a, b and c are shown with their calculated areas. When labeling the area, we include a power of two or a square to the unit of measurement. This means that we multiplied two dimensions (length and width) to find the area. We see this, with the power of 3, when we find the volume of a figure (l x w x h = v). A valid and great question from any student would be, “So for the triangle, what two dimensions are we multiplying for each side, to find the hypotenuse?” Let’s take the same squares and shift them in this manner:
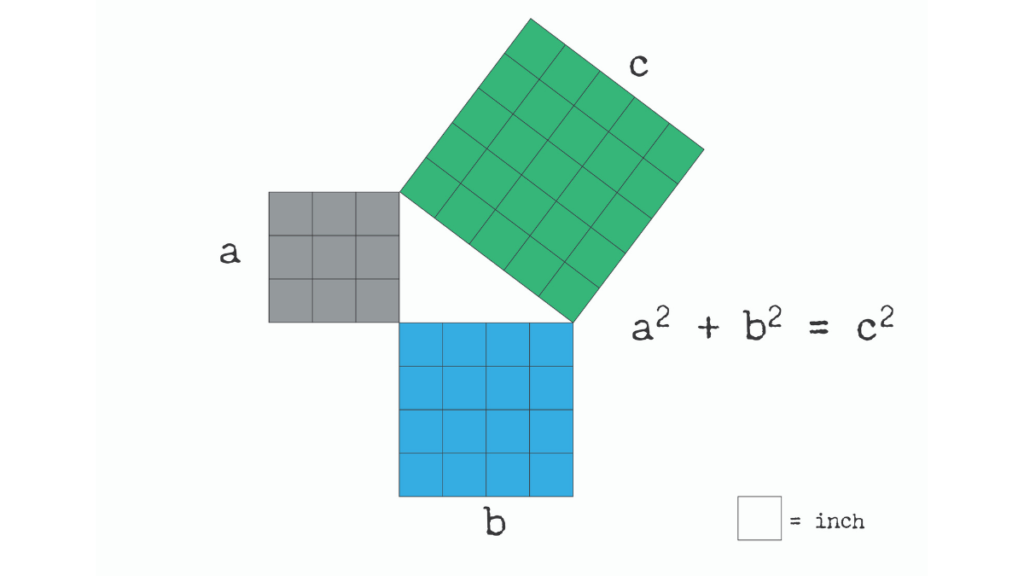
The Pythagorean Theorem in its True Form
This image reveals the key to Pythagoras’ Theorem. Take notice of what is formed in the center of the three squares. Yes, a right triangle. Again, the formula for the Theorem reflects the squares that make up the triangle as much as the triangle itself. Here it is in its entirety:
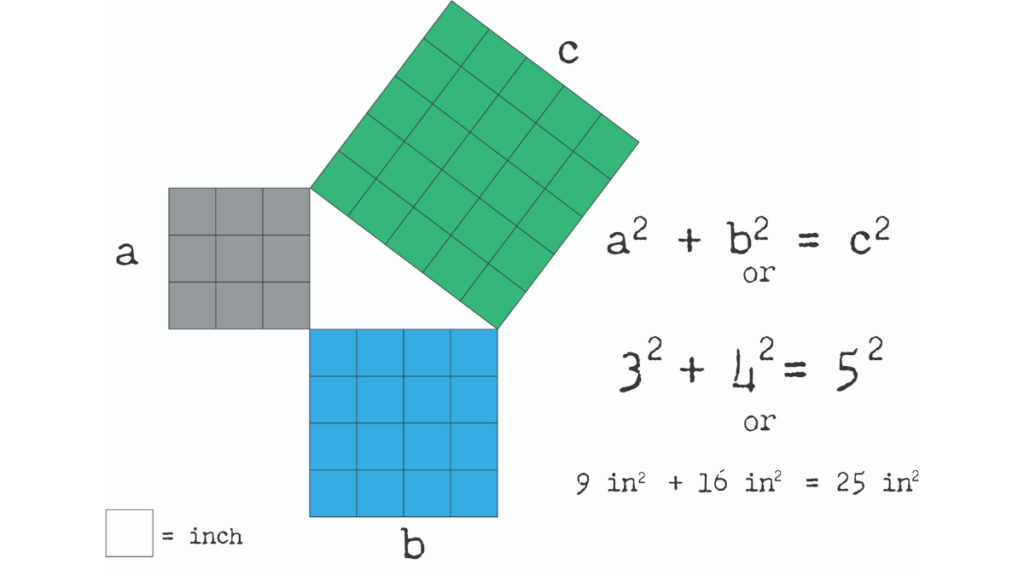
Speaking of theorems, this image is proof that the Pythagorean Theorem is not a2 + b2 = c2. Rather, a2 + b2 = c2 is a formula to prove his theorem to be correct. His theorem basically stated that the area of the square created by the longest side of the triangle (hypotenuse) is equal to the areas of the squares, created by the two legs of the triangle (the two shorter sides), added together. So with the formula, c2 is equal to the area of the square that makes up side c. When the value of c2 is found, the square root of that number is the measurement of c.
How to Help Our Kids
The absence of conceptual understanding is a common root of difficulties with mathematics. Taking the time to learn the building blocks to math concepts saves time in the long run. In addition, it promotes healthy mathematical thinking. Teach that math is so much more than “finding the correct answer”.
The problem that kids more than likely have with the Pythagorean formula is finding the square root of radicals that are not perfect squares. First, have them make a chart of perfect squares and their factors. For example, 1×1=1, 2×2=4, 3×3=9, 4×4=16, etc. This chart can be endless, but keep in mind that most problems given are not going to ask students to find the square root of a number like 1156 (the square root is 34). If their chart goes up to 20×20=400, it should suffice form most problems.
Of course, radicals that are not perfect squares will offer a little more of a challenge. Roots can be estimated by using the perfect square chart. For example, the square root of 12 can be estimated somewhere between 3 and 4, because 12 is between the perfect squares of 9 and 16. The manual work to find the root can be completed through a process of factorization or repeated division. I can write out how this works conceptually in a later article.
For more math help see the following: