Homeschooling
As homeschooling parents, we were so excited to teach mathematics to our children. Without the pressures of timelines and tests, this was our opportunity to teach conceptual math for kids. The right answer is inevitably important, but we are more concerned with our kids’ journey getting to that answer. We want to be sure that they are enjoying the process, and making sense of how the numbers and operations work. Not just work, but how they logically work together. If they are recognizing the connections in what they were seeing and doing, the right answers will eventually come.
How We Were Taught Math
Throughout my education, Mathematics was all about finding the answer to a problem. Through practice, we learned how to efficiently add, subtract, multiply and divide. We were also timed when computing mathematic problems, because speed was just as important as accuracy. Do you remember that feeling, when the teacher passed out the timed multiplication tests? It might not have been advertised but, it was obvious that you were still on the 4s.
As time went on, we learned formulas, rules, and strategies to answer more complex problems. On the class chalkboard, our teacher demonstrated a number of problems for the lesson of the week. We would then open our textbook and complete the practice problems. If we had a book that did not have practice problems, we did the evens and the odds would be for homework. There were a few more pages of this skill in the book. Although, the area of difficulty increased for the application on each page. In addition, the teacher had a weeks worth of blue or black ink dittos for class and home work. The one thing that was certain, we were going to get ample practice with what we were learning. The ideal that “practice makes perfect” is reflected in rote math. Like in sports, the more you practice, the better you will perform.
Conceptual Learning
When we assess a Do It Yourself project for a home improvement task, we can go one of two ways. We can think that it is way over our heads and hire a professional. Or, we can look at it and say to ourselves, “Conceptually, I see how it can be done” and then venture off into a new DIY journey.
When we can conceptually see something, what does that mean? It means that we possess enough experience and knowledge to mentally devise a logical plan. The plan is actually feasible. The plan may not guarantee success, but at least it makes sense. It is one step towards a tangible application, and one step away from the abstract.
What is Abstract?

When we think of something that is abstract, it is natural to imagine something that does not make sense. Why? Because the first thing that comes to our head is an abstract painting. In actuality, an abstract painting is a tangible, concrete image. The only reason why it is abstract is because, we, the viewers, do not recognize it as something that we can accurately label. To the artist, everything makes complete logical sense.
Now consider what happens when we learn the name of the painting and the artist’s thinking behind it. The painting is still classified as an abstract painting, but we now have a different insight when we look at it. For many, we are able to see the thinking or concept of the artist and understand the representation.
“Math is So Abstract”
As an educator, I have heard the comment, “Math is so abstract”. Should I say complaint, rather than comment. If it was a comment, they they are 100% factually correct. As a complaint, they could not be anymore incorrect. Abstract Mathematics is an actual study, but thinking that mathematics is something that does not make sense is erroneous. Unfortunately, that idea comes from the absence of conceptual learning of mathematics.
When students, or adults, do not recognize the practicality of a math problem, it is just like an abstract painting. The problem and the application to solve it is concrete. The difficulty comes from the thinking part of mathematics. No surprises there, right? It is when they can no longer explain how or why the numbers or functions work the way that they do.
Examples of Conceptual Math for Kids
Counting and Addition
Let’s start with the first function of arithmetic, addition. Kids grasp and master the concept of addition because they have a wealth of experience and knowledge of it before they see the plus symbol. As toddlers, kids are able to show knowledge of counting. It may not be verbal but they take notice of quantities. With songs or with grown ups, they then learn to mimic the speech of counting. Later they start making that one to one correspondence with counting and objects. For every number they count, they are adding.

When kids get to addition, manipulatives or objects are used as counters for them to count how many in all. The most popular manipulative are the fingers. At the early stages of addition, kids love to use their fingers to add. At this point of addition, kids are still counting. Addition becomes rote mathematics when they are adding without the aid of manipulatives, only using mental math. Inevitably, rote mathematics is an end goal. As long as it was achieved through the means of conceptual understanding of the function. Through years of counting, we accumulate the experience and knowledge to conceptually understand addition. In other words, we can explain how and why the numbers and function work the way that they do.
Addition and Multiplication
We learned how to add by knowing how to count. We mastered addition to a point that we can effortlessly add mentally. An amazing phenomenon about this mastery is if five people were asked to add 5 + 5 + 5 + 5 + 5 + 5 = _, five different mental strategies might be used to find the answer. One strategy that we learned when counting was skip counting. Skip count by 2s, 5s and 10s were always fun. Skip counting some of the other numbers were more challenging but we still found the patterns (another example of conceptual math).
To further challenge our single digit plus single digit arithmetic, we saw problems such as 2 + 2 + 2 +2 + 4 + 4 + 4 + 9 + 9 + 9 = _. The counters in us solved this by adding 2, 4, 6, 8, 12, 16, 20, 29, 38, 47. The skip counters counted 8 + 12 + 27 = _, 20 + 27 = 47. The teacher may have said, “Wow, you first added the 2s 4 times, then you added the 4s 3 times and then the 9s 3 times“. Later, in 2nd or 3rd grade, the same student will see the problems 2 x 4 = _, 4 x 3 = _ and 9 x 3 = _. Yes, they are the same addition problems, but only in the form of multiplication.

Gold Mine
It is safe to say that multiplication is a juncture in a child’s academic path that can dictate their math outlook. Their progressions with multiplication will guide them through future skills. Conversely, their struggles with multiplication facts will delay their understanding of math progressions. Especially for the skills require the application of multiplication. Not to mention, in schools, speed and accuracy are now factors in mathematics.
Addition is already a mastered skill by the time multiplication is introduced in the curriculum. Conceptually, multiplication is repeated addition. What if kids understood that multiplication is a short cut for a skill that they have already mastered? Somehow this concept gets lost in the process of math progressions. Given the ramifications of this juncture, this is the reason why conceptual math for kids should be a priority.
Slice of Pi

Students drift further away from conceptual mathematics when formulas are introduced for solving problems. Due to the fact that math is now formulaic, students are now just plugging in numbers and applying the functions. Conceptual math for kids begs them to ask, “Why does that formula work?” When finding the circumference of a circle, students multiply 2 times π (3.14) times the radius of the circle. But here is the question that every student should ask, “Where does 3.14 come from?” Believe it or not some teachers say, “It’s part of the formula, just use it”.
Conceptual math for kids will teach them why 3.14 exists when finding the circumference of a circle. Contrary to popular student belief, that some math guy just plugged 3.14 into the formula, there is a very logical explanation.
Starting With What They Know
Before kids get into the formula for finding the circumference of a circle, they should consider what they already know. There are so many connections that can be made throughout math. With that, math concepts should not be taught in isolation from other concepts.
Polygons
When finding the circumference of a circle, students are finding the total distance around the circle. This should sound familiar to them because it is the same idea of finding the perimeter of a two dimensional figure. They first embarked on this with a square. To find the perimeter, or the total distance around the square, they simply added up all of the sides. Since it is a square, students also figure out that they can multiply the equal sides by four to get the perimeter. When they calculate the perimeter of rectangles, they also add up the lengths of each side. The same goes for all polygons.
A Different Two Dimensional Shape

A circle is also a two dimensional shape. Although a circle is not a polygon. A circle is made up of a long curved side. How do we find the perimeter of a circle without sides? First, the distance around a circle is called the circumference. Same idea as a perimeter, just a different name. Second, I will show you that we will find the distance around the circle, through the same process as we would with a polygon. “Impossible,” you may think with a shape absent of sides. It is possible and the answer has always been there. We don’t see the answer because we have been blinded by rote mathematics and formulas.
As mentioned, the formula to find the circumference of a circle is C = 2 π r or C = πd. If only the radius (r) is provided then we would use the first formula. If the diameter (d) is given in the problem, then the second formula is used. Of course, the numerical representation of π is 3.14. Pi actually extends further out than the hundredth place, but for our purposes, using 3.14 is acceptable. For accuracy purposes, scientists and engineers at NASA would use more decimal points beyond .14.
The big question is, “How does 3.14 play a part in finding the circumference of a circle?” It’s a great question and I wish more students would ask it, instead of just following the formula. Conceptual math for kids would approach the answer with more clarity.
Unveiling π
For this part, follow along with the materials. You will need a circle. Any circle will do, but not too big. Although, I assure you that what you will do will work for any circle. You will also need a pipe cleaner or string long enough to create the diameter of the circle. You will also need a pair of scissors and a writing utensil.
Hold the string or pipe cleaner across the middle of the circle, and cut it creating the length of its diameter.

Mark a starting point along the side of the circle. With the string or pipe cleaner, run it from the starting point and form it along the circle, marking where it ends. Mark that section #1.

From the second point, do the same thing and mark the next end point. Mark that section #2.

Again, from the third point do the same thing and mark the next end point. Mark that section #3.

You will notice that your diameter length measurement will go around the circle 3 times, with a little bit of space between sections #1 and #3. Are you starting to see the light? Pi, π, and 3.14 is the number of times the diameter of a circle can go around that circle.

Conceptually Understanding the Formula
So let’s put the formula to use and see how it works. Let’s consider a circle with a radius of 5 ft. We can start of with plugging numbers into the formula C = 2 π r. C = 2 x (times) 3.14 x (times) 5. In this case C = 31.4 ft.
Conceptually, we already have knowledge of how 3.14 plays a part in the circle. To have a full conceptual understanding of this process, we have to take it one step further. Let’s make a connection to something we already know, finding the perimeter of a polygon. We may not have straight sides but we have 3.14 diameter sections around the circle. So if we add these sections, just like a polygon, we would add 10 + 10 +10 + (10 x .14) = C. That translates to three sections of the diameter plus .14 of another diameter. 10 + 10 +10 = 30. The last section is 10 x (times) .14 = 1.4. Put those two answers together, 30 + 1.4 = 31.4 ft. Ladies and gentlemen, that is conceptual math for kids.
Just Multiply it By the Reciprocal
Admittingly, pi was a huge slice to swallow but here is one more conceptual math for kids lesson. One of the easiest concepts to teach is dividing fractions. “Boys and girls, we did such an amazing job with our multiplying fractions test and now we are ready to divide fractions,” encourages the teacher. “I know that some of us don’t like division but watch how easy this will be,” the teacher continues. “You take the second fraction in the problem, flip it over and multiply just like we did on the test,” with an assuring grin.
Once again, this is another example where I would love for any student to raise their hand and inquire about how this process works and how did someone figure that this is how to solve a dividing fractions problem. Instead, excited by the ease of the skill, students proceed with the lesson.
Dividing Fractions
Dividing is not always fun for kids, not to mention neither are fractions. If students are struggling with the dividing fractions, obviously rote mathematics will not help them improve. If you examine a dividing fractions problem, a student can have difficulties with division, multiplication or fractions. In many cases, all three parts are a challenge to students. This is another example of how the lack of conceptual mathematics for kids can lead to an avalanche.
Dividing
Labeling division as either long or short division is the start of a downward slide, away from conceptual mathematics. Both consist of the same process of division but as a student, would you rather do “short” division or “long” division? There is no better way to deter kids from mathematics than giving a concept an intimidating title.
If kids get multiplication conceptually, then the conceptual understanding of division will naturally follow. When kids speed up counting or adding they skip count. When counting by 3s they skip count 5 times to get to reach 15. Division is purely the reverse engineering of multiplication. When you mathematically think of the term “divide” it is exactly the same concept as dividing in general. The objective of division is to split or take apart a whole, to create as many equal groups as possible. How many equal groups can 15 be divided into? 5 or 3 equal groups.
Representations of Division
There are three ways that a division problem can be represented. When we first learned the inverse of multiplication, we were introduced to the “division house or box”. This is the structure that will be utilized for most of our dividing. In the problem below, 15 is the dividend, 5 is the divisor and 3 is the quotient or equal groups.
The next representation of a division problem that we see is through the use of the Obelus symbol, ÷ . The same problem would be written as 15 ÷ 5 = 3. Barring the possibilities of mental math, the division house or box would still have to be used to calculate the quotient.
The final way to show a division problem is through the structure of a fraction. 15/5 = 3 is the same as 15 ÷ 5 = 3. There are two ways that we can visualize answering this form of division. The first way is to remove the numbers from the fraction form and utilize the division house or obelus. The second way to visualize it is to leave it in the fraction form and follow the Identity Property of Division. The property simply states that any number divided by 1 will yield a quotient of the same number. 3 ÷ 1 = 3 or 3/1 =3. In short, any whole number can be written as a fraction by making it a numerator over a denominator of 1. For the problem 15/5, we answer it with the Identity Property in mind. How can we get a denominator of 5, equal to 1? We divide it by 5. To keep the fraction equivalent, we have to divide the numerator, 15, by five as well.
Back to Dividing Fractions
At this point, you may see why I went over the basics of dividing before getting to dividing fractions. If not, here comes the big conceptual reveal. Let’s consider the division problem 3/5 ÷ 1/5 =?. Again, the process will tell us to multiply 3/5 by the reciprocal of 1/5, otherwise known as “keep- change-flip”. Our problem will then become 3/5 x 5/1 = ?. But to understand this conceptually, we need to know why this method solves the problem. Why is the inverse operation of division to multiplication used?
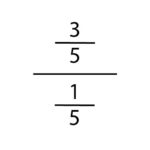
We know that division can be represented in three different ways and we know that we are dealing with fractions. It might seem unconventional but we can rewrite this problem in a fraction divisional form. This is called a complex fraction. 3/5 would be the dividend and would be the numerator and 1/5 is the divisor, the denominator. As a fraction, this may look like a structure that does not make sense. As a division problem, a complex fraction is the model that will explain the the “Keep-Change-Flip” strategy.
Let’s go back to the concept of the Identity Property of Division. We saw that when used on a division problem in the fraction form, the denominator is 1. To get 1/5 equal to one, we have to multiply it by its reciprocal, 5/1. Again, to keep the fraction equivalent, we have to do the same thing to the numerator.
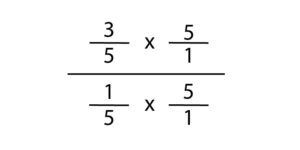
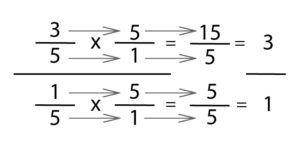
At this point, you can now see why we multiply by the reciprocal when dividing fractions. To complete the problem. Multiply the fractions in the denominator to get product 5/5, or 1. Multiplying the fractions in the numerator will equal 15/5, or 15 ÷ 5 = 3. So your answer to 3/5 ÷ 1/5 = 3. This work will also show students how cross canceling conceptually works.
Conceptual Math for Kids
When we teach conceptual math for kids, we are building the crucial math knowledge and experience that is transferrable to new learning. Without it, new learning is going to be like starting from scratch for many kids.
How Do We do This at Home?
At home, the best way to promote conceptual mathematics for kids is to metaphorically build rice paddies. Put your homeschoolers in situations where they are constantly thinking mathematically. There are application opportunities with gardening, DIY projects, cooking, budgeting and time management. Math is also in the arts, like music, drawing, painting, photography, etc. The mathematics in sports is definitely overlooked. Even toys and games like Legos, Mind Craft, Monopoly, Chess or Battle Ship are beneficial. If you look at theses examples, they mainly consist of an indirect application of math, but their success is contingent on their application.
If you are helping with math concepts that you may not have the confidence to explain in it in detail, there is power in transparency. Just don’t share any negative thoughts that might deter a growth mindset. Research the concept together by referring to some of your favorite resources or videos. Model the metacognition strategies and ask questions like, “Okay, what do we already know or and how much of the process do we understand?” Questioning is actually a really good way to promote active and forward thinking. Also, get to know the 8 Math Practices provided by Common Core. Encourage your homeschoolers to use them when applying math and affirm their use of them when you see it. Each practice does not have to be used for each concept. Identify the ones that would benefit their approach to understanding. Your help will be a great example of Math Practice 1, making sense of problems and persevere in solving them.
There is a sense of satisfaction, diving into the math that we learned as kids and relearning them as math concepts. We get an opportunity to appreciate for the patterns and logic that we overlooked when we were going through countless drills and tests. Although this is a long one, we are only scratching the surface with conceptual math for kids.
Please subscribe for updates on more homeschooling strategies and insights. Also comment below if you want to see conceptual math for kids and the Pythagorean Theorem.
